Table of Contents HIDE
Understanding how defense works in RAID: Shadow Legends can dramatically change the way you see damage reduction in the game. This RAID defense guide and defense calculator will help new players understand one of the game’s key mechanics, which is equally important in both PVE and PVP. Remember, you are almost certainly flooded with questions along the lines of “what is better: passive Geomancer damage reduction or defense buff?“, “what will give greater survivability: a set of shield artifacts or 2000 extra defense points?” These and other similar questions are answered here.
RAID defense video guide
How does defense work in RAID?
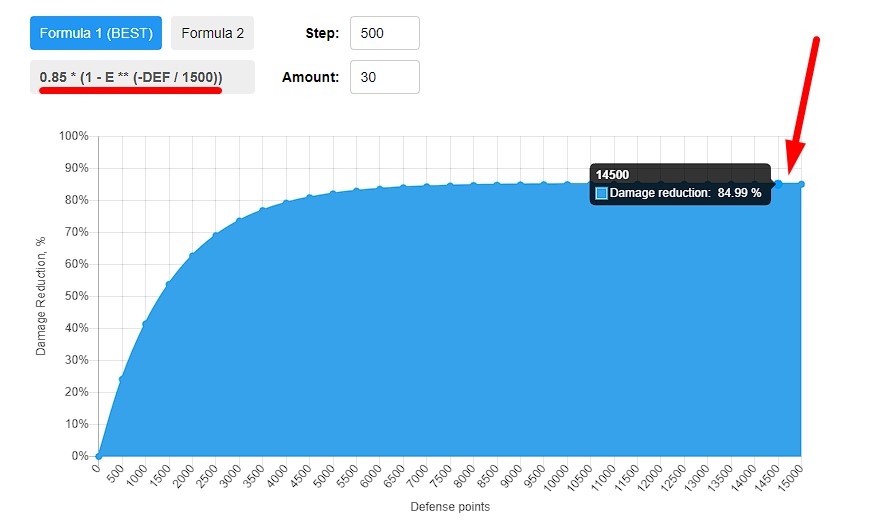
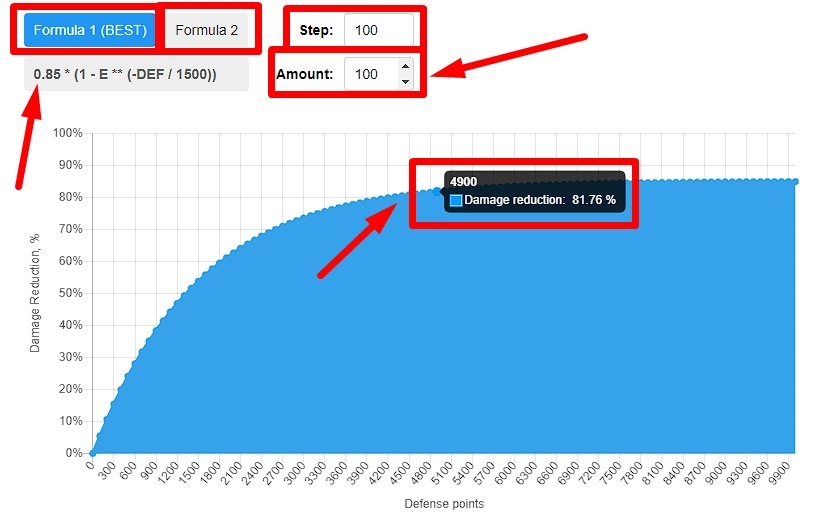
Defense in RAID is represented by the numerical value of DEF, which is present in the characteristics of each hero / boss / mob in the game. The more defense, the less damage the character receives. However, the damage reduction is non-linear with respect to the defense numerical value. In other words, if the hero has 3000 defense, the next 100 points will give a much smaller damage reduction than the same 100 points at 2000 defense for the hero. Using the RAID damage reduction calculator below on this page, you can see this effect as a curve on the graph.
Damage reduction formulas and their rationale
RAID uses some kind of “secret formula” to calculate damage reduction based on defense points. There are at least 3-4 variations of this formula that are walking around the net. Almost all of them are probably invented by the community of players and show roughly the same results. However, there is one formula that looks the most realistic. It was discovered by me on Reddit (as far as I remember, the above post is not the original, but there is also a lot of useful information) a little earlier and repeatedly tested. Personally, I tend to trust it and therefore in my mind it is the reference so far (although I could be wrong).
The formula looks as follows: Mitigation = 0.85 * (1 – E^-DEF/1500), where “^“ denotes the mathematical exponentiation (in a calculator, it looks like «two stars», because in JavaScript mathematical exponentiation is indicated that way) of the numerical constant E, which is approximately ~2.7182. In the original source, at the time the formula was discovered, this constant was longer with more decimal places, but I shortened it to 4 digits because (and I think you would agree with me) we are not too concerned about millionths of damage units. As can be understood from the formula and as can be seen in the screenshot above, this formula has a cap of 85% damage reduction, which cannot be exceeded. This cap is the main argument in favor of the formula’s validity, as it logically fits into the game.
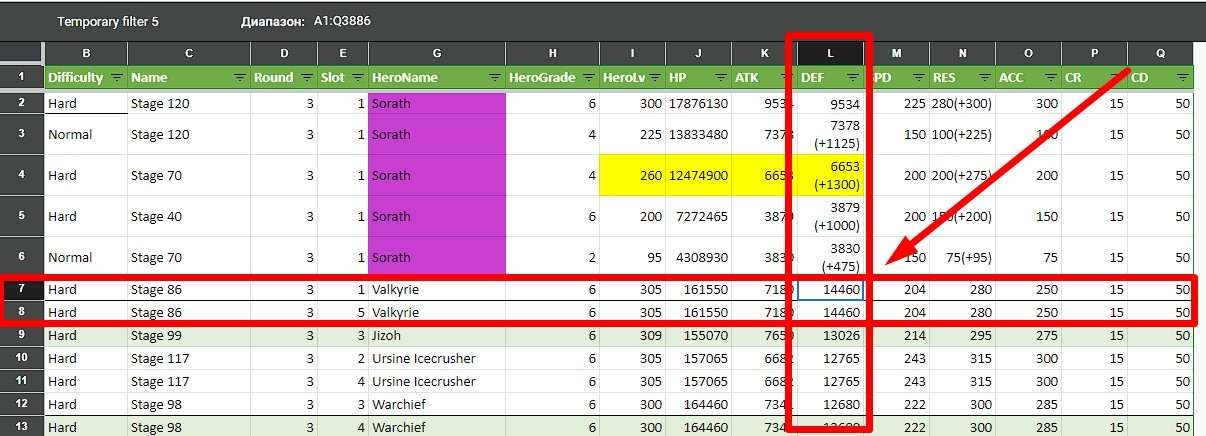
The fact is that the main way the developers from Plarium increase the complexity of bots in the game is to increase their level. For example, in Doom Tower on Hard mode, the level of bots reaches 318, and along with the level, their basic parameters increase significantly. We know this because the real characteristics of a bot were once displayed in the game when you clicked on its portrait in Doom Tower on the command selection screen. And while that feature was soon removed, tables with leaked data from the miners remained online. For example, in this old video the author shows a table with all the stats of mobs and bosses in Doom Tower (you can find it on the author’s Google Drive link or on mine). Even though this table is not maintained and updated, it gives us an idea of what stats the bots have in RAID: Shadow Legends.
The Valkyries have the most defense in this table. It is 14460, which according to this formula is essentially the 85% defense cap. If we imagine that RAID used an alternative formula (invented by the community) – DEF / (DEF + 1250), then the Valkyries would be almost invulnerable to attacks without decreasing defense debuff / ignoring defense, as they would have 23136 (!) points of defense and around 94.87% damage reduction. However, as far as I can personally tell, that is not the case.
Which of the formulas is more reliable is for the esteemed reader to decide. I’ll just add that now, after the release of the hard dungeon floors, we can suggest that one of the reasons why the mobs in them were not enhanced was the technical impossibility of increasing their defense further without changing the damage reduction formula. After all, since defense is tied to level (and Valkyries, as we see, are already capable of achieving 85-95% damage reduction), further increasing the level of the mobs would lead to the inability to deal them any significant damage without damage dealers having the presence of artifact sets or skills that ignore defense, and even if the bot has a 60% decrease defense debuff. A bot with defense in the 25-30k range would be simply impenetrable for the vast majority of heroes in the game. From this, we can draw the logical conclusion that defense reduction in RAID absolutely cannot be linear, and therefore even if the above formulas are not quite accurate, the general principle they model is very correct.
How to check if a formula is working? (proof)
It’s easy to check if any formula works, because you have everything you need: unlimited access to replay any floor of Doom Tower and a defense reduction calculator. All you need to do (if you want to verify it for yourself) is to find out the original damage of the bot on the hero, calculate the reduction for him using the formula and compare the result with the figures you get in the game for other defense values. Let me show you an example.
I will be testing the formulas on the first hard floor of the doom tower on the mob Bulwark, which gets the turn first (and that’s the only reason I chose it). From the table I gave above, we know that Bulwarks has 6993 defenses on the 1st floor of the hard mode. We also know his A2 hit ratio (5.5 * DEF) from the hero database created by the date miners. Accordingly, his initial damage on the hero should be 5.5 * 6993 = ~38462. Since the game has a small random damage spread, which the community usually assumes is +/-10% (although we don’t know for sure), the damage should be in the range of 34616 to 42308.
Then you can take a hero with low defense, for example, Ranger (common) Lvl. 1 and check the actual damage of the mob on it. Due to the spread of damage, this should be done at least 10-20 times, simply restarting the fight after each hit and writing down the numbers of damage received in a table or notebook. It is important to understand that our goal is not to find the arithmetic mean between all these figures, as it might seem. Our goal here is to “farm” 2 numbers: the maximum and minimum, and then find the arithmetic mean between them. This will give the greatest accuracy in the calculations.
After 10 visits, I got the numbers that you can see in the screenshot above. In fact, you can not write them out the same way, but just update the maximum and minimum number. I wrote out the numbers in a column for clarity. So, the arithmetic average between the maximum and minimum number is 36526. Since my long-suffering Ranger has 65 defense points, the damage taken by the heroine according to the main formula is reduced by 3.6%. If we subtract this percentage from the estimated initial damage of the mob, we get 38462 * (1 – 0.036) = 37077. This is very close to the value that was obtained from the tests.
Next, we need to do the same for heroes with more defense. However, before proceeding, make sure that they will not be affected by other possible modifiers (difference in affinity, mastery, passive skills, etc.). I used Andryssia with 2095 defense (~63.97%) and Lightsworn with 4351 defense (~80.33%) for testing. You can see the numbers I received in the picture above. The average damage taken by Andryssia was 13858 (vs. ~13857.86 formula), and the average damage taken by Lightsworn was 7718 (vs. ~7565.48 formula). In my opinion, this is more than enough for the formula to be considered working.
What to do if the mob’s stats are initially unknown?
In this case you can go the opposite way and calculate the estimated initial damage of the mob using the same formula. For example, if the Ranger with 65 defense deals 36526 damage, then we assume that the bot’s initial damage according to the formula should be 36526 / (1 – 0.036) = 37890, which almost corresponds to reality (as we remember, it’s still 38462). Nevertheless, we can take this estimated damage as a basis and run exactly the same test. Even if the damage itself is calculated inaccurately, it will still confirm or deny the validity of the formula. After all, we are not interested in the damage itself, but in how it changes depending on the different values of the numerical defense.
The most important thing about defense you should know
If you do not delve into the mathematics, it may seem quite justified that if the hero’s defense is increased by 10%, then the damage to him will decrease by an additional 10%. In general, it is, but not quite so. The fact is that when we raise defense, we must take into account the ratio of these 10% to the damage that the hero receives without them. Let’s say we have a hero with 50% defense and deal 10000 damage to him, respectively, he will receive only 5000 damage. If we raise his defense to 60%, he will receive another 10% less damage (4000), but his survivability will increase by 1000 / 5000 = 0.2 = 20%. So if we add 10% defense to a hero who took 5000 damage, his survivability will increase by 20%, since he will already take 4000 damage instead of 5000. This is extremely important to understand and digest, and it is included in the calculator that you will find below.
Understanding this difference between increased defense percentages and actual survivability can completely change your game. Suddenly it turns out that the Geomancer passive skill, which reduces damage by 15%, is weaker than just 10% additional damage reduction. This is because it is calculated from the total damage already cut by the defense, while 10% additional defense reduces the overall damage. Suppose a hero with 50% defense is dealt the same 10’000 damage. Then, with 10% additional damage reduction, his survivability, as we have already found out, will increase by 20%. If instead we bet on 15% passive damage reduction, then it turns out that the damage will be reduced to 10000 * 0.5 * (1 – 0.15) = 4250 instead of 4000. So, instead of 20% additional survivability, we will get only these very 750 / 5000 = 0.15 = 15%.
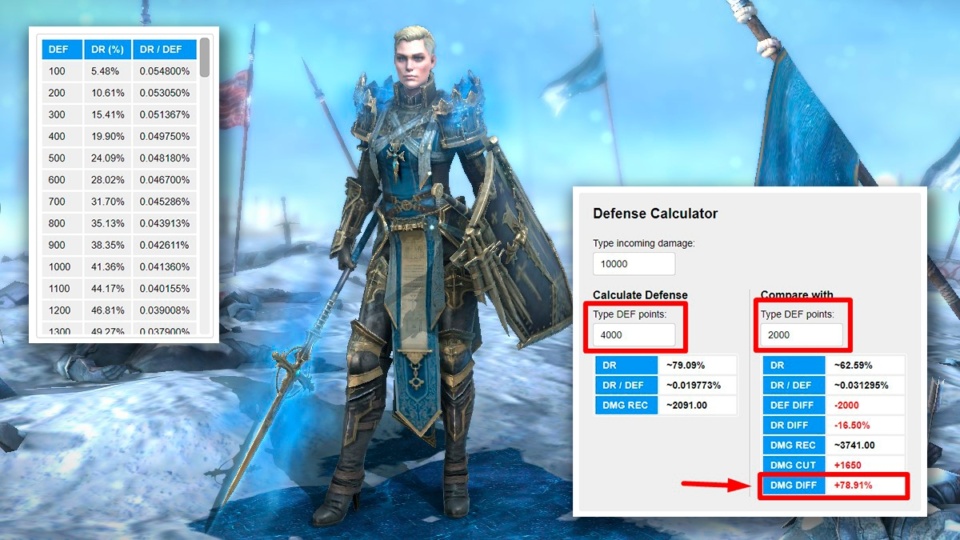
RAID defense calculator
| DR | ~54.51% |
| DR / DEF | ~0.000142% |
| DMG REC | 40314 |
| DR | ~54.51% |
| DR / DEF | ~0.000142% |
| DMG REC | 40314 |
| DEF DIFF | 323 |
| DR DIFF | ~6.92% |
| DMG CUT | 11422 |
| DMG DIFF | ~8.92% |
How to use
When you hover over any field or cell with a designation, a tooltip with an explanation will appear.
At the top of the calculator, you can see the 2 formulas mentioned in the article. You can switch between them. This is done so that you can use the one you trust more.
Below is a damage reduction graph that you can change in real time. To do this, there are Step fields above it (the number of defense points that will be a step between the points on the chart; it must be more than 10) and Amount (the number of points themselves on the chart). You can change these values to see how the damage reduction curve changes. This is mainly for display purposes. However, you can hover over any point on the graph and get more information.
Under the graph on the left is a table in which all points on the graph are entered. It consists of three columns:
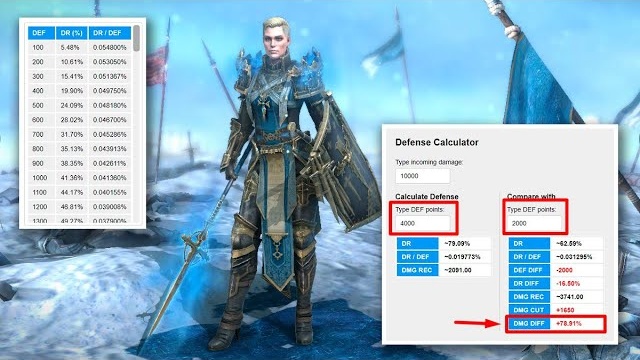
- DEF – defense points
- DR (%) – damage reduction calculated according to the current formula
- DR / DEF – the percentage of damage reduction that you receive for 1 defense point with the current value of the hero’s defense (calculated by simply dividing the second field by the first)
This table will help you understand what defense value is optimal for you, and whether it is worth increasing it further.
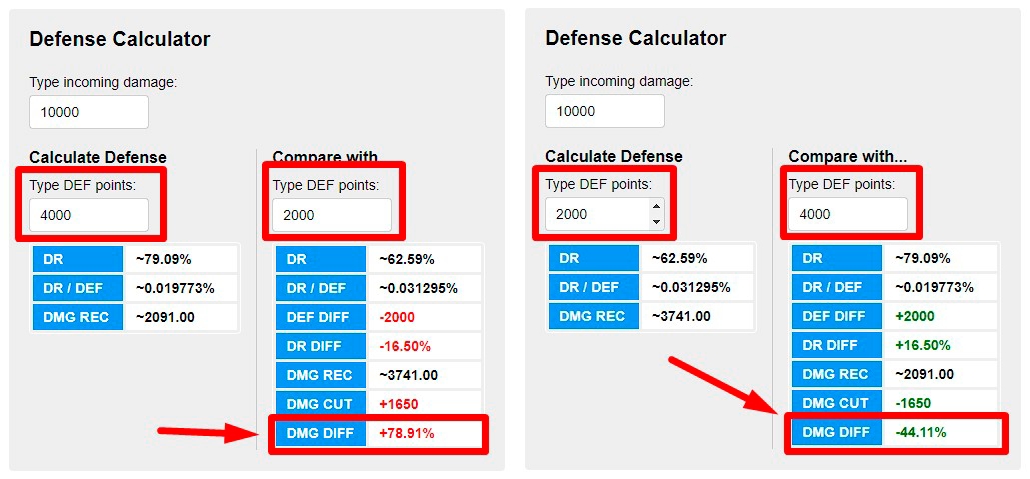
To the right of the table is the calculator itself. It contains 3 fields in which you can enter test damage on the hero, his defense and modified defense in order to compare the results. The tables below show the results of the calculations. In addition to those already known to you, the tables contain the following notation:
- DMG REC is the damage that the hero will receive with the current amount of defense points in accordance with the current formula
- DEF DIFF is the difference between the defense values that are entered in the fields
- DR DIFF is the percentage damage reduction difference (calculated by simply subtracting the first value from the second)
- DMG CUT – integer difference in damage taken (calculated by simply subtracting the first value from the second)
- DMG DIFF is the percentage difference between the damage that the player will receive with the DEF value from the first field and with the DEF value from the second (calculated using the formula (1 – (100 – dmgReduction2) / (100-dmgReduction1)) * 100 ).
DMG DIFF is the most important field in the calculator, for which it was, in fact, created. It shows how much less or more damage the hero will actually receive when changing his defense. If you compare the mirror results (for example, enter 2000 DEF and 4000 DEF and then swap them), you will see that DMG DIFF is very different. This may seem like a mistake, but it’s not. Remember that the value of this cell is always calculated relative to the first DR, so it can and must change. After all, it is easy to calculate that if 2091 is increased by 78.91%, it will turn out just 2091 * 1.7891 = 3741, if 3741 is reduced by 44.11%, it will again be 3741 * (1 – 0.4411) = 2091. I know that this may be difficult to understand and fit in your head… Therefore, just accept it 😉.